Giả sử chúng ta có một danh sách cạnh của một đồ thị có hướng, có n nút và tên nút từ 0 đến n- 1. Chúng ta cũng có hai giá trị nguyên a và b. Chúng ta phải kiểm tra xem có bất kỳ nút c nào để chúng ta có thể đi từ c đến a và cũng có thể từ c đến b.
Vì vậy, nếu đầu vào giống như
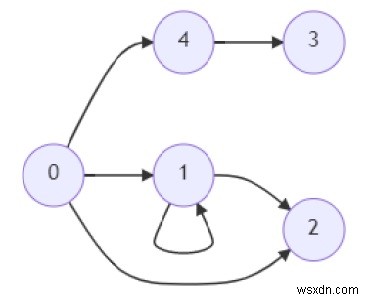
Và a =2, b =3, thì đầu ra sẽ là True, vì ở đây c =0, nên chúng ta có tuyến đường từ 0 đến 2 và cũng từ 0 đến 3.
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -
- Xác định một hàm DFS (). Điều này sẽ lấy biểu đồ, nút, đã truy cập
- nếu nút không được truy cập, thì
- đánh dấu nút là đã truy cập
- đối với mỗi x trong biểu đồ [nút], thực hiện
- DFS (đồ thị, x, đã truy cập)
- Từ phương pháp chính, hãy thực hiện như sau -
- graph:=tạo danh sách gần kề từ edge_list
- visit_a, Visit_b:=hai tập hợp trống
- DFS (đồ thị, a, đã thăm_a)
- DFS (đồ thị, b, đã thăm_b)
- ans:=một danh sách mới từ giao điểm của Visit_b và visit_a
- nếu ans không trống, thì
- trả về True
- trả về Sai
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def edge_list_to_graph(edges): s = set() for x, y in edges: s.add(x) s.add(y) s = len(list(s)) graph = [[] for x in range(s)] for x, y in edges: graph[y].append(x) return graph def DFS(graph, node, visited): if node not in visited: visited.add(node) for x in graph[node]: DFS(graph, x, visited) def solve(edges, a, b): graph = edge_list_to_graph(edges) visited_a, visited_b = set(), set() DFS(graph, a, visited_a) DFS(graph, b, visited_b) ans = list(visited_a.intersection(visited_b)) if ans: return True return False ed_list = [(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)] a = 2 b = 3 print(solve(ed_list, a, b))
Đầu vào
[(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)], 2, 3
Đầu ra
True
