Giả sử chúng ta có một số n. Nếu chúng ta có các số như [1,2, ..., n], chúng ta phải đếm số BST có thể được tạo thành bằng cách sử dụng n giá trị này. Nếu câu trả lời quá lớn, hãy sửa đổi kết quả theo 10 ^ 9 + 7.
Vì vậy, nếu đầu vào là n =3, thì đầu ra sẽ là 14,
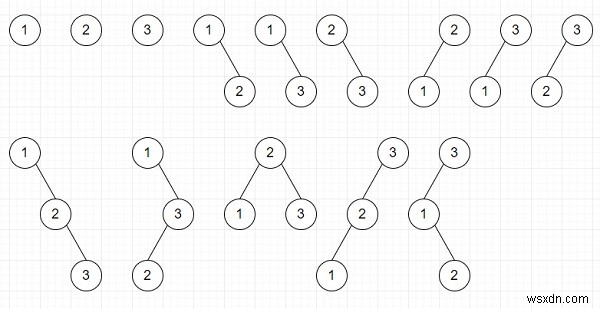
Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau
- a:=một danh sách có các giá trị [0, 1]
- m:=10 ^ 9 + 7
- max_n:=1000
- đối với k trong phạm vi 2 đến max_n + 1, thực hiện
- insert (1 + tổng của tất cả các phần tử của danh sách (a [i] * a [k - i] với mọi i trong phạm vi (1, k))) mod m vào cuối a
- return (a [n + 1] - 1) mod m
Ví dụ
Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -
def solve(n):
a = [0, 1]
m = 10**9+7
max_n = 1000
for k in range(2, max_n + 2):
a.append((1 + sum(a[i] * a[k - i] for i in range(1, k))) % m)
return ((a[n + 1] - 1) % m)
n = 3
print(solve(n)) Đầu vào
3
Đầu ra
14
