Số lần nghịch đảo diễn ra để Sắp xếp mảng đã cho được gọi là số lần nghịch đảo. vấn đề đảo ngược là một bài toán cổ điển có thể được giải quyết bằng cách sử dụng Thuật toán sắp xếp hợp nhất. trong bài toán này v chúng ta sẽ đếm tất cả các phần tử nhiều hơn nó ở bên trái của nó và thêm số lượng vào đầu ra. ThisLogic được thực hiện bên trong chức năng hợp nhất của sắp xếp hợp nhất.
Để hiểu chủ đề tốt hơn, chúng ta hãy lấy một ví dụ. Chúng ta hãy xem xét hai mảng con tham gia vào quá trình hợp nhất -



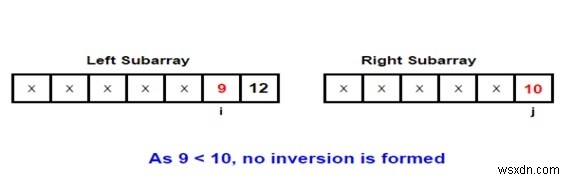
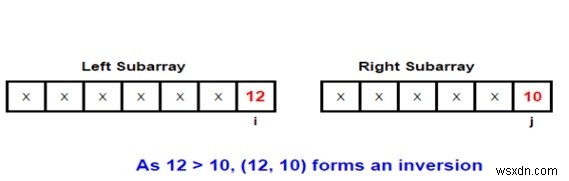
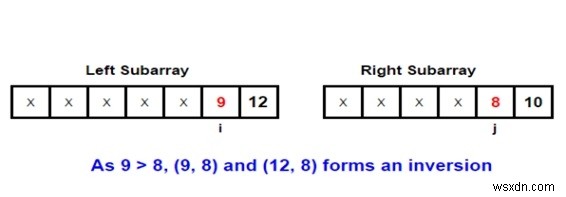
Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5 Giải thích
Số lượng nghịch đảo của một mảng
Cho một mảng, hãy tìm số nghịch đảo của nó. Nếu (i
Ví dụ:
Có 5 nghịch đảo trong mảng
(9,6), (9,4), (9,5), (6,4), (6,5)
1. So sánh các giá trị của phần tử với nhau.
2. Tăng bộ đếm nếu giá trị ở chỉ số thấp hơn cao hơn.
3. Hiển thị kết quả.
Ví dụ
#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
int k = low, i = low, j = mid + 1;
int inversionCount = 0;
while (i <= mid && j <= high) {
if (arr[i] <= arr[j]) {
aux[k++] = arr[i++];
} else {
aux[k++] = arr[j++];
inversionCount += (mid - i + 1); // NOTE
}
}
while (i <= mid)
aux[k++] = arr[i++];
for (int i = low; i <= high; i++)
arr[i] = aux[i];
return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
if (high == low) // if run size == 1
return 0;
int mid = (low + ((high - low) >> 1));
int inversionCount = 0;
inversionCount += MergeSort(arr, aux, low, mid);
inversionCount += MergeSort(arr, aux, mid + 1, high);
inversionCount += Merge(arr, aux, low, mid, high);
return inversionCount;
}
int main() {
int arr[] = { 1, 9, 6, 4, 5 };
int N = 5;
int aux[N];
for (int i = 0; i < N; i++)
aux[i] = arr[i];
printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
return 0;
} 