Giả sử chúng ta có một đồ thị với một số nút và các cạnh được kết nối. Mỗi cạnh có trọng số nhị phân. Vì vậy, trọng số sẽ là 0 hoặc 1. Một đỉnh nguồn được đưa ra. Chúng ta phải tìm đường đi ngắn nhất từ nguồn đến bất kỳ đỉnh nào khác. Giả sử đồ thị như dưới đây -
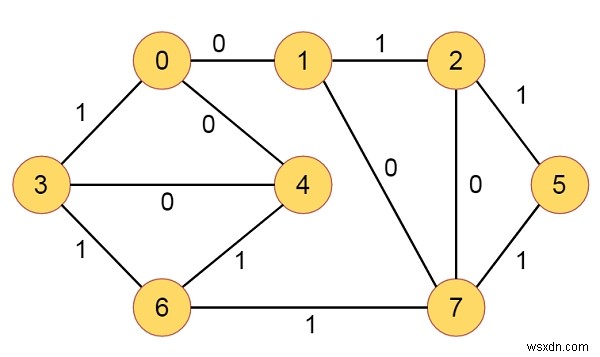
Trong thuật toán BFS thông thường, tất cả các trọng số cạnh đều giống nhau. Ở đây một số là 0 và một số là 1. Trong mỗi bước, chúng tôi sẽ kiểm tra điều kiện khoảng cách tối ưu. Ở đây chúng ta sẽ sử dụng hàng đợi kết thúc kép để lưu trữ nút. Vì vậy, chúng tôi sẽ kiểm tra trọng lượng cạnh. Nếu nó là 0, thì đẩy nó ở phía trước, nếu không thì ở phía sau. Hãy để chúng tôi kiểm tra thuật toán để có ý tưởng tốt hơn.
Thuật toán
binaryBFS (src) -
begin define dist array to store source to vertex i into dist[i]. Initially fill with infinity dist[src] := 0 insert src into queue Q. v := first element from Q, and delete it from queue while Q is not empty, do for all connected edge e of v, do if the weight of v to next of i > dist[v] + weight of v to i weight, then update the weight if the weight is 0, then store to front, otherwise back end if done done print all distance from dist array end
Ví dụ
#include<iostream>
#include<vector>
#include<deque>
#define V 8
using namespace std;
struct node {
int next, weight;
};
vector <node> edges[V];
void binaryBFS(int src) {
int dist[V];
for (int i=0; i<V; i++) //initially set as infinity
dist[i] = INT_MAX;
deque <int> Q;
dist[src] = 0; //distance from source to source is 0
Q.push_back(src);
while (!Q.empty()) {
int v = Q.front(); //delete first vertex, and store to v
Q.pop_front();
for (int i=0; i<edges[v].size(); i++) {
//check optimal distance
if (dist[edges[v][i].next] > dist[v] + edges[v][i].weight) {
dist[edges[v][i].next] = dist[v] + edges[v][i].weight;
if (edges[v][i].weight == 0) //0 weight edge is stored at front, otherwise at back
Q.push_front(edges[v][i].next);
else
Q.push_back(edges[v][i].next);
}
}
}
for (int i=0; i<V; i++)
cout << dist[i] << " ";
}
void addEdge(int u, int v, int wt) {
edges[u].push_back({v, wt});
edges[v].push_back({u, wt});
}
int main() {
addEdge(0, 1, 0);
addEdge(0, 3, 1);
addEdge(0, 4, 0);
addEdge(1, 2, 1);
addEdge(1, 7, 0);
addEdge(2, 5, 1);
addEdge(2, 7, 0);
addEdge(3, 4, 0);
addEdge(3, 6, 1);
addEdge(4, 6, 1);
addEdge(5, 7, 1);
addEdge(6, 7, 1);
int src = 6;
binaryBFS(src);
} Đầu ra
1 1 1 1 1 2 0 1
