Sản phẩm của các phạm vi trong một mảng trong C

Được đưa ra với mảng, L, R, P làm đầu vào và nhiệm vụ là tìm phạm vi giữa L và R với sản phẩm theo mô-đun làm đầu ra và hiển thị nó

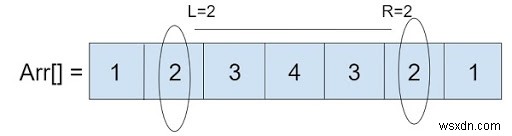
Như đã cho trong hình, chúng ta có mảng các phần tử và L là giá trị Bên trái là 2 và R là giá trị Bên phải là 2. Bây giờ chương trình phải tìm các tích của các phạm vi giữa chúng.

Ví dụ

Input-:  A[] = { 1, 2, 3, 4, 5, 6 }
   P = 29  L = 2 R = 6
Output-: 24
Input-: A[] = {1, 2, 3, 4, 5, 6},
   L = 2 R = 5 P = 113
Output-: 7

Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau -

Lấy các giá trị đầu vào trong một mảng các phần tử nguyên, Giá trị bên trái (L), giá trị bên phải (R) và P (giá trị nguyên tố)
Bắt đầu duyệt các phần tử từ giá trị Trái sang giá trị Phải
Tiếp tục lưu trữ phép nhân trong một biến tạm thời
Tiếp tục thực hiện hoạt động mô-đun với giá trị nguyên tố
In kết quả cuối cùng

Thuật toán

Start
Step 1 -> declare function to calculate product
   int calculateProduct(int A[], int L,int R, int P)
      declare variable as int i
         set L = L – 1
         set R = R – 1
      declare int ans = 1
      Loop For i = L and i <= R and i++
         Set ans = ans * A[i]
         Set ans = ans % P
      End
      return ans
Step 2-> In main()
   Declare an array as int A[] = { 1, 2, 3, 4, 5, 6 }
   Declare variable as int P = 29
   Declare variable as int L = 2, R = 6
   Print A, L, R, P
Stop

Ví dụ

#include <stdio.h>
int calculateProduct(int A[], int L,int R, int P) {
   int i;
   //Because array starts with 0 and
   //L R starts from 1.
   L = L - 1;
   R = R - 1;
   int ans = 1;
   for ( i = L; i <= R; i++) {
      ans = ans * A[i];
      ans = ans % P;
   }
   return ans;
}
int main() {
   int A[] = { 1, 2, 3, 4, 5, 6 };
   int P = 29;
   int L = 2, R = 6;
      printf("%d\n", calculateProduct(A, L, R, P));
   return 0;
}

Sản phẩm của các phạm vi trong một mảng trong C

Ví dụ

Thuật toán

Ví dụ

Đầu ra