Mô tả chương trình
Số ngũ giác là một số trong ô thứ năm của bất kỳ hàng nào trong tam giác Pascal bắt đầu bằng hàng 5 số hạng 1 4 6 4 1 từ trái sang phải hoặc từ phải sang trái.
Một vài số đầu tiên thuộc loại này là
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365
Số Pentatope thuộc loại số tượng hình, có thể được biểu diễn dưới dạng các mẫu hình học đều đặn, rời rạc. Công thức cho số ngũ phân thứ n là
$$ \ left (\ begin {array} {c} n + 3 \\ 4 \ end {array} \ right) =\ left (\ frac {n (n + 1) + (n + 2) + (n + 3)} {24} \ right) =\ left (\ frac {n ^ 2} {4!} \ Right) $$
Thuật toán
Chấp nhận Thuật ngữ thứ N từ Người dùng để tìm Số ngũ vị trí.
Sử dụng công thức
$$ \ left (\ begin {array} {c} n + 3 \\ 4 \ end {array} \ right) =\ left (\ frac {n (n + 1) + (n + 2) + (n + 3)} {24} \ right) =\ left (\ frac {n ^ 2} {4!} \ Right) $$
Ví dụ
/* Program to print pentatope numbers upto Nth term */
#include<stdio.h>
int main() {
int n, n1, nthterm, nthterm1, i;
clrscr();
printf("\n Please enter the nth term to print Pentatope: ");
scanf("%d",&n);
nthterm = n * (n + 1) * (n + 2) * (n + 3) / 24;
printf("The Pentotpe Number is: ");
printf("%d", nthterm);
printf("\n\n");
printf("Printing the Pentotope Numbers upto Nth Term");
printf("\n Print Pentatope Numbers till the term: ");
scanf("%d",&n1);
printf("\n\n");
printf("The Pentotope Numbers are:");
printf("\n\n");
for (i = 1; i <= n1; i++){
nthterm1 = (i * (i + 1) * (i + 2) * (i + 3) / 24);
printf("%d\t", nthterm1);
}
getch();
return 0;
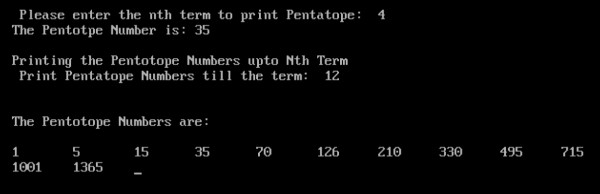
} Đầu ra