Giải quyết vấn đề N-Queens với Ruby

N-Queens là một thử thách mã hóa thú vị, nơi bạn phải đặt N nữ hoàng trên một bảng N * N .

Nó trông như thế này:

Nữ hoàng có thể di chuyển theo mọi hướng:

• Dọc
• Ngang
• Đường chéo

Giải pháp (có thể có nhiều) phải đặt tất cả các quân hậu trên bàn cờ &mọi nữ hoàng phải nằm ngoài tầm với của mọi nữ hoàng khác.

Trong bài viết này, bạn sẽ tìm hiểu cách tôi đưa ra giải pháp.

Kế hoạch

Khi giải quyết những thách thức này, nơi tốt nhất để bắt đầu là viết ra một kế hoạch bằng tiếng Anh đơn giản.

Điều này giúp bạn hiểu rõ vấn đề là gì và các bước giải quyết.

Nếu bạn gặp khó khăn khi viết kế hoạch của mình, hãy đảm bảo rằng bạn hiểu vấn đề 100% .

Kế hoạch của tôi cho giải pháp N-Queens:

• Bắt đầu @ vị trí 0,0
• nếu vị trí hợp lệ:đặt nữ hoàng, cột trước (+ 1), đặt hàng thành 0
  • kiểm tra trên cùng, dưới cùng, trái, phải, đường chéo
• else:đặt trước 1 ô vuông
  • đi lên (hàng + 1) trừ khi vị trí hiện tại ==n
  • lùi lại khi không thể đặt nữ hoàng vào cột hiện tại
    • loại bỏ nữ hoàng cuối cùng
    • đặt hàng &cột thành vị trí cuối cùng của nữ hoàng với hàng + 1

Đây là phiên bản rõ ràng hơn của những gì tôi đã viết ra ban đầu.

Tôi đi sâu vào các bước cần thêm chi tiết trước khi có thể triển khai chúng.

Bây giờ :

Kế hoạch của bạn sẽ không hoàn hảo (của tôi thì không) nhưng nó sẽ cung cấp cho bạn ý tưởng về những gì cần làm.

Nếu bạn không thể viết một kế hoạch chắc chắn thì không có gì sai khi tra cứu giải pháp …

… Hiểu cách giải pháp hoạt động sau đó viết giải pháp của riêng bạn.

Tìm chuyển động hợp lệ

Để kiểm tra xem một vị trí có hợp lệ hay không, chúng ta phải xem xét theo một số hướng.

Thay vì làm lộn xộn với một bảng 2D, tôi quyết định có một loạt các nữ hoàng trong hội đồng quản trị với các vị trí của họ.

Sau đó, chúng tôi kiểm tra mảng nữ hoàng này so với vị trí mà chúng tôi muốn xác thực.

Ví dụ:đối với kiểm tra hàng:

def queen_in_row(row)
  @queens_in_board.find { |r, c| r == row }
end

Điều này sẽ trả về một nữ hoàng nếu hàng được lấy hoặc bằng không nếu không.

Bạn không phải kiểm tra xem cột có trống không vì chúng tôi chuyển sang cột tiếp theo sau khi đặt một nữ hoàng .

Đối với các đường chéo, cần thêm một số công việc vì có 4 trong số chúng.

Đây là mã cho đường chéo phía trên bên phải:

def right_upper_diagonal_for(row, column, n)
  diagonals = []

  until row == n || column == n
    diagonals << [row += 1, column += 1]
  end

  diagonals
end

Các đường chéo khác cũng vậy, điểm khác biệt duy nhất là ở điều kiện của vòng lặp và hướng (hàng + 1 / hàng - 1).

Điều này cần một chút thử nghiệm và sai sót để làm đúng, nhưng không sao cả.

Điều quan trọng là phải kiểm tra các phương pháp này một cách riêng biệt để đảm bảo chúng hoạt động . Khi bạn có một tập hợp các phương pháp làm việc, bạn có thể kết hợp chúng lại với nhau để tạo thành giải pháp hoàn chỉnh của mình.

Đây là phương pháp tập hợp tất cả các đường chéo &kiểm tra với mọi quân hậu trong bàn cờ:

def queen_in_diagonal(row, column, n)
  diagonals =
    right_upper_diagonal_for(row, column, n) +
    left_upper_diagonal_for(row, column, n) +
    left_lower_diagonal_for(row, column, n) +
    right_lower_diagonal_for(row, column, n)


  diagonals.any? { |r, c| r == row && c == column } ||
  diagonals.any? { |r, c| @queens_in_board.any? { |qr, qc| r == qr && c == qc } }
end

Cách triển khai BackTracking

Để giải quyết những thách thức không hề nhỏ này đòi hỏi bạn phải biết một cái nhìn sâu sắc, kỹ thuật hoặc thuật toán.

Trong trường hợp N-Queens kỹ thuật đang quay ngược lại .

Backtracking là hoàn tác một số hành động trước đó (như đặt nữ hoàng trên bàn cờ) &thử lại với một cấu hình khác.

Tôi nghĩ đây sẽ là phần khó nhất, nhưng hóa ra lại khá dễ dàng.

Để tìm ra điều này, tôi đã chạy một mô phỏng nhỏ.

Tôi đã tự vẽ cho mình một bảng và một số hộp chống lại các nữ hoàng :

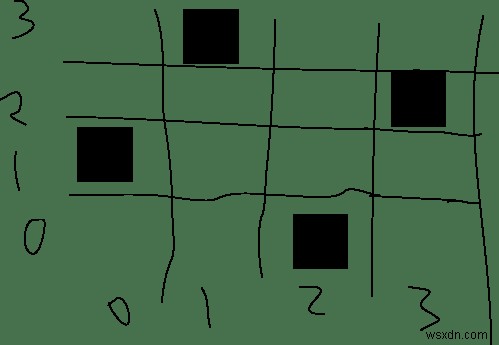
Sau đó, tôi chỉ cần di chuyển các hộp xung quanh bảng (trực tiếp bằng chuột của tôi) để mô phỏng thuật toán.

Đây là mã:

while row >= n
  row    = @queens_in_board[-1][0] + 1
  column = @queens_in_board[-1][1]

  puts "Backtracking, deleted: #{@queens_in_board.pop}"
end

Bạn cũng có thể làm điều này cho các vấn đề khác khi bạn gặp khó khăn, vẽ nó trên một số chương trình vẽ hoặc thậm chí trên giấy và chơi với nó.

Đây là bản chất của cách hoạt động của điều này:

• Chúng tôi tiếp tục đi lên, nếu chúng tôi đạt đến đầu bảng điều đó có nghĩa là chúng tôi không thể xếp được nữ hoàng trên cột này
• Chúng tôi lùi lại bằng cách đặt vị trí hiện tại thành quân hậu cuối cùng và xóa nó khỏi bảng
• Nếu chúng tôi không thể đặt nữ hoàng từ vị trí này, chúng tôi sẽ lùi lại một lần nữa

+ 1 trên vị trí hàng là cách chúng tôi thúc đẩy quân hậu cuối cùng để đặt lại vị trí của nó &mở cấu hình bo mạch mới.

Khi chạy mã này cho n =4 (không có giải pháp nào cho n =2 &n =3):

"placing at 0 0"
"placing at 2 1"
Backtracking, deleted: [2, 1]
"placing at 3 1"
"placing at 1 2"
Backtracking, deleted: [1, 2]
Backtracking, deleted: [3, 1]
Backtracking, deleted: [0, 0]
"placing at 1 0"
"placing at 3 1"
"placing at 0 2"
"placing at 2 3"

Ảnh gif này là một ví dụ trực quan về thuật toán:

Mã đầy đủ

def solve_n_queens(n)
  @queens_in_board = []

  row = 0
  column = 0

  until @queens_in_board.size == n
    if queen_in_row(row) || queen_in_diagonal(row, column, n)
      row += 1

      while row >= n
        row    = @queens_in_board[-1][0] + 1
        column = @queens_in_board[-1][1]

        puts "Backtracking, deleted: #{@queens_in_board.pop}"
      end
    else
      place_queen(row, column)

      p "placing at #{row} #{column}"

      row = 0
      column += 1
    end
  end

  @queens_in_board
end

def queen_in_row(row)
  @queens_in_board.find { |r, c| r == row }
end

def queen_in_diagonal(row, column, n)
  diagonals =
    right_upper_diagonal_for(row, column, n) +
    left_upper_diagonal_for(row, column, n) +
    left_lower_diagonal_for(row, column, n) +
    right_lower_diagonal_for(row, column, n)


  diagonals.any? { |r, c| r == row && c == column } ||
  diagonals.any? { |r, c| @queens_in_board.any? { |qr, qc| r == qr && c == qc } }
end

def top_row?(row, n)
  row == n
end

def place_queen(row, column)
  @queens_in_board << [row, column]
end

def right_upper_diagonal_for(row, column, n)
  diagonals = []

  until row == n || column == n
    diagonals << [row += 1, column += 1]
  end

  diagonals
end

def left_upper_diagonal_for(row, column, n)
  diagonals = []

  until row == n || column == 0
    diagonals << [row += 1, column -= 1]
  end

  diagonals
end

def right_lower_diagonal_for(row, column, n)
  diagonals = []

  until row == 0 || column == n
    diagonals << [row -= 1, column += 1]
  end

  diagonals
end

def left_lower_diagonal_for(row, column, n)
  diagonals = []

  until row == 0 || column == 0
    diagonals << [row -= 1, column -= 1]
  end

  diagonals
end

def print_board(n)
  board = Array.new(n) { Array.new(n) { "." } }

  @queens_in_board.each { |queen| board[queen[0]][queen[1]] = "Q" }

  board.map { |n| n.join("|") }.reverse
end

p solve_n_queens(4)
p solve_n_queens(5)

puts print_board(5)

Phiên bản đệ quy

Đây là phiên bản thay thế tìm TẤT CẢ các giải pháp khả thi.

def solve_n_queens(n, column = 0, queens_in_board = [])
  @queens_in_board = queens_in_board

  n.times do |row|
    unless queen_in_row(row) || queen_in_diagonal(row, column, n)
      place_queen(row, column)

      solve_n_queens(n, column + 1, @queens_in_board)

      remove_last_queen
    end
  end

  puts print_board(n) if @queens_in_board.size == n
end

Điều duy nhất thay đổi là solve_n_queens phương pháp.

Phiên bản này sử dụng đệ quy (một phương thức gọi chính nó) để khám phá tất cả các giải pháp từng phần.

Khi tìm thấy một giải pháp hoàn chỉnh, chúng tôi in nó bằng cách sử dụng print_board phương pháp.

Tóm tắt

Bạn đã tìm hiểu về thử thách mã hóa N-Queens và cách giải quyết nó trong Ruby. Bạn cũng đã học được cách cải thiện kỹ năng giải quyết vấn đề của mình.

Nếu bạn thích bài viết này, hãy chia sẻ nó với bất kỳ ai có thể hưởng lợi từ nó.

Cảm ơn vì đã đọc!