Khái niệm
Đối với Cây tìm kiếm nhị phân cân bằng đã cho và tổng mục tiêu, chúng tôi viết một hàm trả về true nếu có một cặp có tổng bằng với tổng đích, nếu không thì trả về false. Trong trường hợp này, độ phức tạp về thời gian dự kiến là O (n) và chỉ có thể thực hiện thêm khoảng trống O (Logn). Tại đây, không cho phép bất kỳ sửa đổi nào đối với Cây tìm kiếm nhị phân.Chúng tôi phải lưu ý rằng chiều cao của BST cân bằng luôn là O (Logn).
Ví dụ
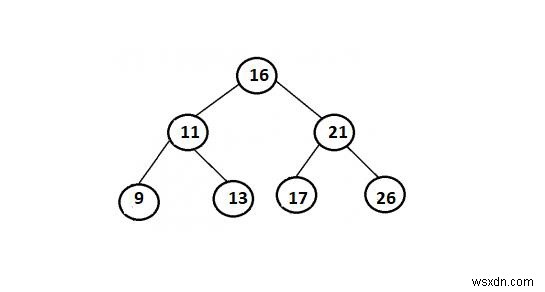
Phương pháp
Theo Giải pháp Brute Force, chúng tôi xem xét từng cặp trong BST và xác minh xem tổng có bằng X. Độ phức tạp về thời gian của giải pháp này sẽ là O (n ^ 2).
Bây giờ, một giải pháp tốt hơn là xây dựng một mảng phụ trợ và lưu trữ lượng truyền tải Inorder của BST trong mảng. Trong trường hợp này, mảng sẽ được sắp xếp dưới dạng truyền tải nhỏ hơn của BST luôn tạo ra dữ liệu được sắp xếp. Vì vậy, sau khi có sẵn đường truyền inorder, chúng ta có thể ghép nối trong thời gian O (n). Hãy nhớ rằng, giải pháp này hoạt động trong thời gian O (n), nhưng yêu cầu không gian phụ trợ O (n).
Ví dụ
// Java code to find a pair with given sum
// in a Balanced BST
import java.util.ArrayList;
// A binary tree node
class Node1 {
int data1;
Node1 left1, right1;
Node1(int d){
data1 = d;
left1 = right1 = null;
}
}
public class BinarySearchTree {
// Indicates root of BST
Node1 root1;
// Indicates constructor
BinarySearchTree(){
root1 = null;
}
// Indicates inorder traversal of the tree
void inorder(){
inorderUtil1(this.root1);
}
// Indicates utility function for inorder traversal of the tree
void inorderUtil1(Node1 node1){
if (node1 == null)
return;
inorderUtil1(node1.left1);
System.out.print(node1.data1 + " ");
inorderUtil1(node1.right1);
}
// Now this method mainly calls insertRec()
void insert(int key1){
root1 = insertRec1(root1, key1);
}
/* Indicates a recursive function to insert a new key in BST */
Node1 insertRec1(Node1 root1, int data1){
/* So if the tree is empty, return a new node */
if (root1 == null) {
root1 = new Node1(data1);
return root1;
}
/* Otherwise, recur down the tree */
if (data1 < root1.data1)
root1.left1 = insertRec1(root1.left1, data1);
else if (data1 > root1.data1)
root1.right1 = insertRec1(root1.right1, data1);
return root1;
}
// Indicates method that adds values of given BST into ArrayList
// and hence returns the ArrayList
ArrayList<Integer> treeToList(Node1 node1, ArrayList<Integer> list1){
// Indicates Base Case
if (node1 == null)
return list1;
treeToList(node1.left1, list1);
list1.add(node1.data1);
treeToList(node1.right1, list1);
return list1;
}
// Indicates method that checks if there is a pair present
boolean isPairPresent(Node1 node1, int target1){
// Now this list a1 is passed as an argument
// in treeToList method
// which is later on filled by the values of BST
ArrayList<Integer> a1 = new ArrayList<>();
// Now a2 list contains all the values of BST
// returned by treeToList method
ArrayList<Integer> a2 = treeToList(node1, a1);
int start1 = 0; // Indicates starting index of a2
int end1 = a2.size() - 1; // Indicates ending index of a2
while (start1 < end1) {
if (a2.get(start1) + a2.get(end1) == target1) // Target Found!{
System.out.println("Pair Found: " + a2.get(start1) + " + " + a2.get(end1) + " " + "= " + target1);
return true;
}
if (a2.get(start1) + a2.get(end1) > target1)
// decrements end
{
end1--;
}
if (a2.get(start1) + a2.get(end1) < target1)
// increments start
{
start1++;
}
}
System.out.println("No such values are found!");
return false;
}
// Driver function
public static void main(String[] args){
BinarySearchTree tree1 = new BinarySearchTree();
/*
16
/ \
11 21
/ \ / \
9 13 17 26 */
tree1.insert(16);
tree1.insert(11);
tree1.insert(21);
tree1.insert(9);
tree1.insert(13);
tree1.insert(17);
tree1.insert(26);
tree1.isPairPresent(tree1.root1, 34);
}
} Đầu ra
Pair Found: 13 + 21 = 34
