Ghi nhớ là một kỹ thuật dựa trên lập trình động được sử dụng để cải thiện hiệu suất của một thuật toán đệ quy bằng cách đảm bảo rằng phương pháp này không chạy cho cùng một tập hợp đầu vào nhiều lần bằng cách lưu giữ bản ghi kết quả cho các đầu vào đã cung cấp (được lưu trữ trong một mảng). Có thể đạt được sự tối ưu hóa bằng cách triển khai cách tiếp cận từ trên xuống của phương pháp đệ quy.
Hãy để chúng tôi hiểu tình huống này với sự trợ giúp của ví dụ Fibonacci cơ bản
Ghi nhớ 1-D
Chúng ta sẽ xem xét một thuật toán đệ quy chỉ có một tham số không hằng số (chỉ một tham số thay đổi giá trị của nó) do đó phương pháp này được gọi là ghi nhớ 1-D. Đoạn mã sau đây là để tìm N’th (tất cả các từ cho đến N) trong chuỗi Fibonacci.
Ví dụ
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
} Đầu ra
NẾU chúng ta chạy đoạn mã trên với n =5, nó sẽ tạo ra kết quả sau.
Calculating fibonacci number for: 5 Calculating fibonacci number for: 4 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2 Calculating fibonacci number for: 2 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2
Giá trị Fibonacci cho n =5:5
Cần lưu ý rằng số Fibonacci cho 2 và 3 được tính nhiều lần. Hãy để chúng tôi hiểu rõ hơn bằng cách vẽ một cây đệ quy cho chuỗi Fibonacci của điều kiện trên, tức là n =5.
Ở đây hai nút con sẽ đại diện cho lệnh gọi đệ quy mà nó thực hiện. Như có thể thấy F (3) và F (2) được tính toán nhiều lần và có thể tránh được kết quả vào bộ nhớ đệm sau mỗi bước.
Chúng tôi sẽ sử dụng một bộ memoize biến thể hiện để lưu vào bộ nhớ đệm kết quả. Đầu tiên nó được kiểm tra xem n đã có trong Bộ memoize chưa, nếu có thì giá trị được trả về và nếu không thì giá trị sẽ được tính toán và thêm vào tập hợp.
Ví dụ
import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
public int fibMemoize(int input) {
if (input == 0)
return 0;
if (input == 1)
return 1;
if (this.memoizeSet.containsKey(input)) {
System.out.println("Getting value from computed result for " + input);
return this.memoizeSet.get(input);
}
int result = fibMemoize(input - 1) + fibMemoize(input - 2);
System.out.println("Putting result in cache for " + input);
this.memoizeSet.put(input, result);
return result;
}
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
public static void main(String[] args) {
TutorialPoint tutorialPoint = new TutorialPoint();
System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
}
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra Kết quả sau
Adding result in memoizeSet for 2 Adding result in memoizeSet for 3 Getting value from computed result for 2 Adding result in memoizeSet for 4 Getting value from computed result for 3 Adding result in memoizeSet for 5
Giá trị Fibonacci cho n =5:5
Như có thể thấy số Fibonacci cho 2 và 3 không được tính lại. Ở đây chúng tôi giới thiệu một bản ghi nhớ HashMap để lưu trữ các giá trị đã được tính toán trước khi mọi phép tính Fibonacci được kiểm tra trong tập hợp nếu đối với đầu vào, giá trị đã được tính toán và nếu không giá trị cho đầu vào cụ thể được thêm vào tập hợp.
Ghi nhớ 2-D
Chương trình trên chúng ta chỉ có một tham số không phải là hằng số. Trong chương trình dưới đây, chúng tôi sẽ lấy một ví dụ về một chương trình đệ quy có hai tham số thay đổi giá trị của nó sau mỗi lần gọi đệ quy và chúng tôi sẽ thực hiện ghi nhớ trên hai tham số không hằng số để tối ưu hóa nó. Đây được gọi là Ghi nhớ 2-D.
Ví dụ:-Chúng tôi sẽ triển khai Trình tự con chung dài nhất tiêu chuẩn (LCS) Nếu một tập hợp các trình tự được đưa ra, bài toán con chung dài nhất là tìm một dãy con chung của tất cả các chuỗi có độ dài tối đa. Các kết hợp có thể có sẽ là 2n.
Ví dụ
class TP {
static int computeMax(int a, int b) {
return (a > b) ? a : b;
}
static int longestComSs(String X, String Y, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + longestComSs(X, Y, m - 1, n - 1);
else
return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
}
public static void main(String[] args) {
String word_1 = "AGGTAB";
String word_2 = "GXTXAYB";
System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
}
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra Kết quả sau
Length of LCS is 4
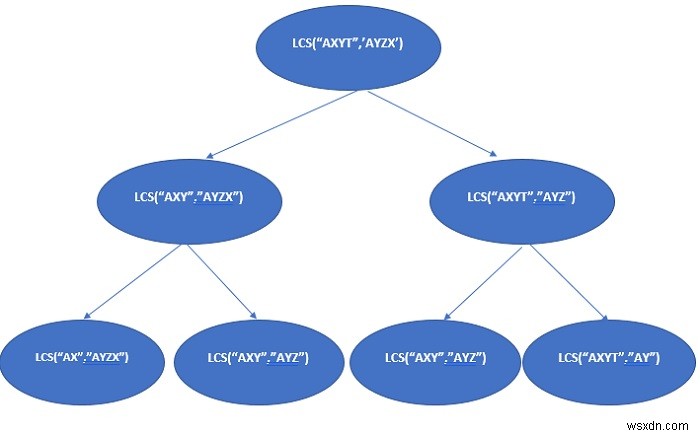
Trong cây đệ quy nửa đường ở trên, lcs ("AXY", "AYZ") được giải nhiều lần.
Do thuộc tính Cấu trúc con chồng chéo của bài toán này, có thể tránh tính toán trước các bài toán con giống nhau bằng cách sử dụng tính năng Ghi nhớ hoặc Lập bảng.
Phương pháp ghi nhớ của mã đệ quy được thực hiện như sau.
Ví dụ
import java.io.*;
import java.lang.*;
class testClass {
final static int maxSize = 1000;
public static int arr[][] = new int[maxSize][maxSize];
public static int calculatelcs(String str_1, String str_2, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (arr[m - 1][n - 1] != -1)
return arr[m - 1][n - 1];
if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
return arr[m - 1][n - 1];
}
else {
int a = calculatelcs(str_1, str_2, m, n - 1);
int b = calculatelcs(str_1, str_2, m - 1, n);
int max = (a > b) ? a : b;
arr[m - 1][n - 1] = max;
return arr[m - 1][n - 1];
}
}
public static void main(String[] args) {
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
arr[i][j] = -1;
}
}
String str_1 = "AGGTAB";
String str_2 = "GXTXAYB";
System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
}
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra Kết quả sau
Length of LCS is 4
Phương pháp tiếp cận
Người ta đã thấy rằng trong phương thức (máy tính) có 4 đối số với 2 đối số là hằng số (không ảnh hưởng đến Ghi nhớ) và 2 đối số không phải là hằng số (m và n) thay đổi giá trị của nó trong mỗi lần gọi phương thức đệ quy. Vì vậy, để đạt được sự Ghi nhớ, chúng tôi giới thiệu một mảng 2-D để lưu trữ các giá trị được tính toán của lcs (m, n) tại arr [m-1] [n-1]. Chúng tôi không thực hiện bất kỳ lệnh gọi đệ quy nào nữa và trả về arr [m-1] [n-1] bất cứ khi nào hàm có cùng đối số m và n được gọi lại, vì tính toán trước đó của lcs (m, n) đã được thực hiện được lưu trữ trong arr [m-1] [n-1], do đó giảm thiểu số lượng lệnh gọi đệ quy.
Ghi nhớ 3-D
Đây là một cách tiếp cận để đạt được sự Ghi nhớ cho một chương trình đệ quy có 3 đối số không hằng số. Ở đây chúng tôi đang lấy ví dụ về tính toán Độ dài LCS cho ba chuỗi.
Cách tiếp cận ở đây là tạo ra tất cả các chuỗi con có thể có (Tổng số chuỗi con có thể có là 3ⁿ) cho các chuỗi đã cho và khớp với chuỗi con chung dài nhất trong số chúng.
Chúng tôi sẽ giới thiệu một bảng 3-D để lưu trữ các giá trị được tính toán. Xem xét các dãy con.
-
A1 [1 ... i] i
-
A2 [1 ... j] j
-
A3 [1 ... k] k
Nếu chúng ta tìm thấy một ký tự chung (X [i] ==Y [j] ==Z [k]), chúng ta cần lặp lại các ký tự còn lại. Hoặc chúng ta sẽ tính toán tối đa các trường hợp sau
-
Để lại X [i] định kỳ cho những người khác
-
Để lại Y [j] cho những người khác
-
Để lại Z [k] định kỳ cho những người khác
Vì vậy, nếu chúng ta hình thành ý tưởng trên trong hàm đệ quy thì
f (N, M, K) ={1 + f (N-1, M-1, K-1) if (X [N] ==Y [M] ==Z [K] max (f (N- 1, M, K), f (N, M-1, K), f (N, M, K-1))}
-
f (N-1, M, K) =Để X [i] lặp lại cho những người khác
-
f (N, M-1, K) =Để lại Y [j] cho những người khác
-
f (N, M, K-1) =Để Z [k] lặp lại cho những người khác
Ví dụ
import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
public static int[][][] arr = new int[100][100][100];
static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
arr[i][j][0] = 0;
}
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= o; j++) {
arr[0][i][j] = 0;
}
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= o; j++) {
arr[i][0][j] = 0;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= o; k++) {
if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
}
else {
arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
}
}
}
}
return arr[m][n][o];
}
static int calculateMax(int a, int b, int c) {
if (a > b && a > c)
return a;
if (b > c)
return b;
return c;
}
public static void main(String[] args) {
String str_1 = "clued";
String str_2 = "clueless";
String str_3 = "xcxclueing";
int m = str_1.length();
int n = str_2.length();
int o = str_3.length();
System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
}
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra Kết quả sau
Length of LCS is 4
