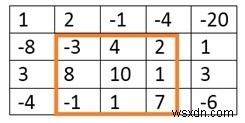
Một ma trận được đưa ra. Chúng ta cần tìm một ma trận hình chữ nhật (đôi khi là hình vuông), có tổng là lớn nhất.
Ý tưởng đằng sau thuật toán này là cố định các cột bên trái và bên phải và cố gắng tìm tổng của phần tử từ cột bên trái sang cột bên phải cho mỗi hàng và lưu trữ nó tạm thời. Chúng tôi sẽ cố gắng tìm số hàng trên cùng và dưới cùng. Sau khi có được mảng tạm thời, chúng ta có thể áp dụng Thuật toán Kadane để có được mảng con tổng tối đa. Với nó, tổng hình chữ nhật sẽ được tạo thành.
Đầu vào và Đầu ra
Input: The matrix of integers. 1 2 -1 -4 -20 -8 -3 4 2 1 3 8 10 1 3 -4 -1 1 7 -6 Output: The top left point and bottom right point of the submatrix, and the total sum of the submatrix. (Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29
Thuật toán
kadaneAlgorithm (mảng, bắt đầu, kết thúc, n)
Đầu vào: Mảng sẽ chứa tổng, điểm đầu và điểm cuối, số phần tử.
Đầu ra - Tìm điểm bắt đầu và điểm kết thúc.
Begin sum := 0 and maxSum := - ∞ end := -1 tempStart := 0 for each element i in the array, do sum := sum + array[i] if sum < 0, then sum := 0 tempStart := i + 1 else if sum > maxSum, then maxSum := sum start := tempStart end := i done if end ≠ -1, then return maxSum maxSum := array[0], start := 0 and end := 0 for each element i from 1 to n of array, do if array[i] > maxSum, then maxSum := array[i] start := i and end := i done return maxSum End
maxSumRect (Ma trận)
Đầu vào: Ma trận đã cho.
Đầu ra: tổng lớn nhất của hình chữ nhật.
Begin maxSum := - ∞ define temp array, whose size is same as row of matrix for left := 0 to number of columns in the Matrix, do till temp array with 0s for right := left to column of matrix -1, do for each row i, do temp[i] := matrix[i, right] done sum := kadaneAlgorithm(temp, start, end, number of rows) if sum > maxSum, then maxSum := sum endLeft := left endRight := right endTop := start endBottom := end done done display top left and bottom right corner and the maxSum End
Ví dụ
#include<iostream>
#define ROW 4
#define COL 5
using namespace std;
int M[ROW][COL] = {
{1, 2, -1, -4, -20},
{-8, -3, 4, 2, 1},
{3, 8, 10, 1, 3},
{-4, -1, 1, 7, -6}
};
int kadaneAlgo(int arr[], int &start, int &end, int n) { //find max sum and starting and ending location
int sum = 0, maxSum = INT_MIN;
end = -1; //at first no place is selected
int tempStart = 0; //starting from 0
for (int i = 0; i < n; i++) {
sum += arr[i];
if (sum < 0) {
sum = 0;
tempStart = i+1;
}else if (sum > maxSum) { //get maximum sum, and update start and end index
maxSum = sum;
start = tempStart;
end = i;
}
}
if (end != -1)
return maxSum;
//when all elements are negative in the array
maxSum = arr[0];
start = end = 0;
// Find the maximum element in array
for (int i = 1; i < n; i++) {
if (arr[i] > maxSum) {
maxSum = arr[i];
start = end = i;
}
}
return maxSum;
}
void maxSumRect() {
int maxSum = INT_MIN, endLeft, endRight, endTop, endBottom;
int left, right;
int temp[ROW], sum, start, end;
for (left = 0; left < COL; left++) {
for(int i = 0; i<ROW; i++)//temp initially holds all 0
temp[i] = 0;
for (right = left; right < COL; ++right) {
for (int i = 0; i < ROW; ++i) //for each row, find the sum
temp[i] += M[i][right];
sum = kadaneAlgo(temp, start, end, ROW); //find sum of rectangle (top, left) and (bottom right)
if (sum > maxSum) { //find maximum value of sum, then update corner points
maxSum = sum;
endLeft = left;
endRight = right;
endTop = start;
endBottom = end;
}
}
}
cout << "(Top, Left) ("<<endTop<<", "<<endLeft<<")"<<endl;
cout << "(Bottom, Right) ("<<endBottom<<", "<<endRight<<")"<<endl;
cout << "The max sum is: "<< maxSum;
}
int main() {
maxSumRect();
} Đầu ra
(Top, Left) (1, 1) (Bottom, Right) (3, 3) The max sum is: 29