Chương trình C ++ để triển khai danh sách gần kề

Biểu diễn danh sách kề của một đồ thị là biểu diễn danh sách được liên kết. Trong biểu diễn này chúng ta có một mảng danh sách Kích thước mảng là V. Ở đây V là số đỉnh. Nói cách khác, chúng ta có thể nói rằng chúng ta có một mảng để lưu trữ V số lượng danh sách khác nhau. Nếu tiêu đề danh sách là đỉnh u, thì nó biểu thị rằng nó sẽ chứa tất cả các đỉnh liền kề của u.

Sự phức tạp của việc biểu diễn Danh sách gần kề

• Biểu diễn này nhận O (V + 2E) cho đồ thị vô hướng và O (V + E) cho đồ thị có hướng. Nếu số lượng các cạnh được tăng lên, thì không gian cần thiết cũng sẽ được tăng lên.

Đầu vào :

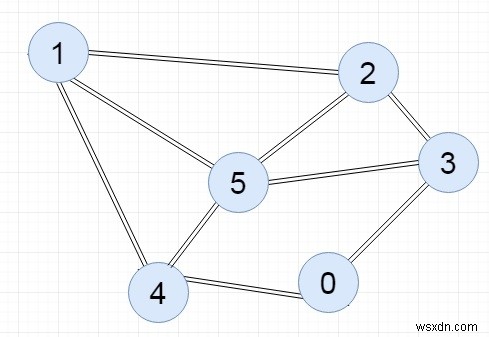
Đầu ra :

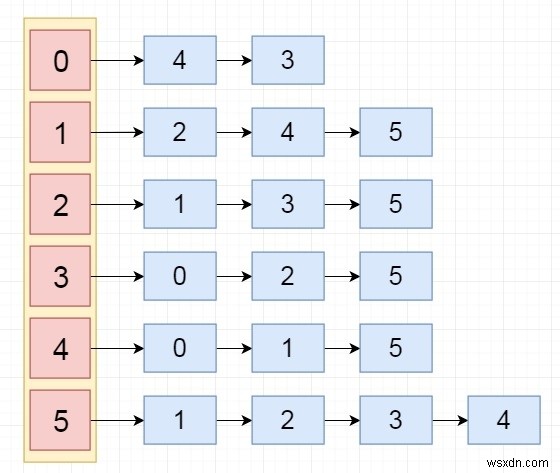
Thuật toán

add_edge (adj_list, u, v)

Đầu vào :Chữ u và v của cạnh {u, v} và danh sách kề

Đầu ra :Danh sách gần kề của biểu đồ G

Begin
   Append v into the list at index u
   Append u into the list at index v
End

Mã mẫu

#include<iostream>
#include<list>
#include<iterator>
using namespace std;
void displayAdjList(list<int> adj_list[], int v) {
   for(int i = 0; i<v; i++) {
      cout << i << "--->";
      list<int> :: iterator it;
      for(it = adj_list[i].begin(); it != adj_list[i].end(); ++it) {
         cout << *it << " ";
      }
      cout << endl;
   }
}
void add_edge(list<int> adj_list[], int u, int v) {    //add v into the list u, and u into list v
   adj_list[u].push_back(v);
   adj_list[v].push_back(u);
}
main(int argc, char* argv[]) {
   int v = 6;    //there are 6 vertices in the graph
   //create an array of lists whose size is 6
   list<int> adj_list[v];
   add_edge(adj_list, 0, 4);
   add_edge(adj_list, 0, 3);
   add_edge(adj_list, 1, 2);
   add_edge(adj_list, 1, 4);
   add_edge(adj_list, 1, 5);
   add_edge(adj_list, 2, 3);
   add_edge(adj_list, 2, 5);
   add_edge(adj_list, 5, 3);
   add_edge(adj_list, 5, 4);
   displayAdjList(adj_list, v);
}

Đầu ra

0--->4 3
1--->2 4 5
2--->1 3 5
3--->0 2 5
4--->0 1 5
5--->1 2 3 4