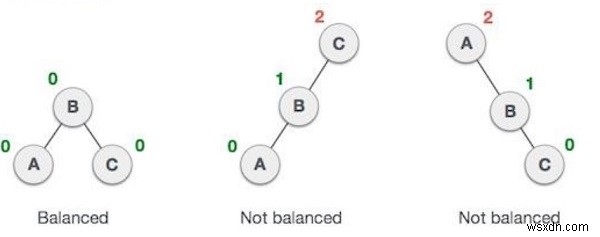
Cây AVL là một Cây tìm kiếm nhị phân tự cân bằng trong đó sự khác biệt giữa chiều cao của các cây con bên trái và bên phải không được nhiều hơn một cho tất cả các nút
Xoay cây là một thao tác thay đổi cấu trúc mà không can thiệp vào thứ tự của các phần tử trên cây AVL. Nó di chuyển một nút lên trên cây và một nút xuống dưới. Nó được sử dụng để thay đổi hình dạng của cây và giảm chiều cao của nó bằng cách di chuyển các cây con nhỏ hơn xuống và các cây con lớn hơn lên, dẫn đến cải thiện hiệu suất của nhiều hoạt động trên cây. Hướng của một vòng quay phụ thuộc vào phía mà các nút cây được dịch chuyển trong khi những người khác nói rằng nó phụ thuộc vào con nào chiếm vị trí của gốc. Đây là một chương trình C ++ để triển khai Cây AVL.
Mô tả chức năng:
chiều cao (trung bình *) :Nó tính toán chiều cao của cây AVL đã cho.
chênh lệch (avl *) :Nó tính toán sự khác biệt giữa chiều cao của các cây con của cây đã cho
avl * rr_rotat (avl *) :Xoay phải là sự kết hợp của xoay phải sau đó xoay phải.
avl * ll_rotat (avl *) :Xoay trái phải là sự kết hợp của xoay trái sau đó xoay trái.
avl * lr_rotat (avl *) :Xoay trái-phải là sự kết hợp giữa xoay trái và xoay phải.
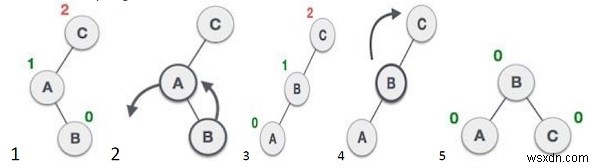
avl * rl_rotat (avl *) :Nó là sự kết hợp giữa xoay phải sau đó xoay trái.
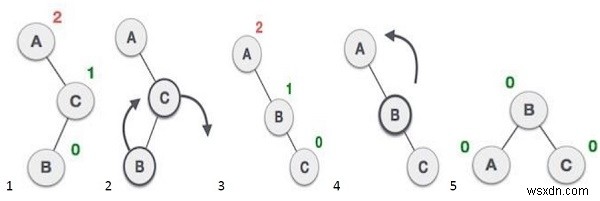
Số dư avl * (avl *): Nó thực hiện hoạt động cân bằng đối với cây bằng cách lấy hệ số cân bằng
avl * insert (avl *, int) :Nó thực hiện thao tác chèn. Chèn các giá trị vào cây bằng cách sử dụng chức năng này.
hiển thị (avl *, int) :Nó hiển thị các giá trị của cây.
inorder (avl *) :Đi ngang cây theo thứ tự.
đặt hàng trước (avl *) :Đi ngang cây theo cách đặt hàng trước.
đơn đặt hàng bưu điện (avl *) :Đi ngang cây theo thứ tự sau.
Ví dụ
#include<iostream>
#include<cstdio>
#include<sstream>
#include<algorithm>
#define pow2(n) (1 << (n))
using namespace std;
struct avl {
int d;
struct avl *l;
struct avl *r;
}*r;
class avl_tree {
public:
int height(avl *);
int difference(avl *);
avl *rr_rotat(avl *);
avl *ll_rotat(avl *);
avl *lr_rotat(avl*);
avl *rl_rotat(avl *);
avl * balance(avl *);
avl * insert(avl*, int);
void show(avl*, int);
void inorder(avl *);
void preorder(avl *);
void postorder(avl*);
avl_tree() {
r = NULL;
}
};
int avl_tree::height(avl *t) {
int h = 0;
if (t != NULL) {
int l_height = height(t->l);
int r_height = height(t->r);
int max_height = max(l_height, r_height);
h = max_height + 1;
}
return h;
}
int avl_tree::difference(avl *t) {
int l_height = height(t->l);
int r_height = height(t->r);
int b_factor = l_height - r_height;
return b_factor;
}
avl *avl_tree::rr_rotat(avl *parent) {
avl *t;
t = parent->r;
parent->r = t->l;
t->l = parent;
cout<<"Right-Right Rotation";
return t;
}
avl *avl_tree::ll_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = t->r;
t->r = parent;
cout<<"Left-Left Rotation";
return t;
}
avl *avl_tree::lr_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = rr_rotat(t);
cout<<"Left-Right Rotation";
return ll_rotat(parent);
}
avl *avl_tree::rl_rotat(avl *parent) {
avl *t;
t= parent->r;
parent->r = ll_rotat(t);
cout<<"Right-Left Rotation";
return rr_rotat(parent);
}
avl *avl_tree::balance(avl *t) {
int bal_factor = difference(t);
if (bal_factor > 1) {
if (difference(t->l) > 0)
t = ll_rotat(t);
else
t = lr_rotat(t);
}
else if (bal_factor < -1) {
if (difference(t->r) > 0)
t= rl_rotat(t);
else
t = rr_rotat(t);
}
return t;
}
avl *avl_tree::insert(avl *r, int v) {
if (r == NULL) {
r= new avl;
r->d = v;
r->l = NULL;
r->r= NULL;
return r;
}
else if (v< r->d) {
r->l= insert(r->l, v);
r = balance(r);
}
else if (v >= r->d) {
r->r= insert(r->r, v);
r = balance(r);
}
return r;
}
void avl_tree::show(avl *p, int l) {
int i;
if (p != NULL) {
show(p->r, l+ 1);
cout<<" ";
if (p == r)
cout << "Root -> ";
for (i = 0; i < l&& p != r; i++)
cout << " ";
cout << p->d;
show(p->l, l + 1);
}
}
void avl_tree::inorder(avl *t) {
if (t == NULL)
return;
inorder(t->l);
cout << t->d << " ";
inorder(t->r);
}
void avl_tree::preorder(avl *t) {
if (t == NULL)
return;
cout << t->d << " ";
preorder(t->l);
preorder(t->r);
}
void avl_tree::postorder(avl *t) {
if (t == NULL)
return;
postorder(t ->l);
postorder(t ->r);
cout << t->d << " ";
}
int main() {
int c, i;
avl_tree avl;
while (1) {
cout << "1.Insert Element into the tree" << endl;
cout << "2.show Balanced AVL Tree" << endl;
cout << "3.InOrder traversal" << endl;
cout << "4.PreOrder traversal" << endl;
cout << "5.PostOrder traversal" << endl;
cout << "6.Exit" << endl;
cout << "Enter your Choice: ";
cin >> c;
switch (c) {
case 1:
cout << "Enter value to be inserted: ";
cin >> i;
r= avl.insert(r, i);
break;
case 2:
if (r == NULL) {
cout << "Tree is Empty" << endl;
continue;
}
cout << "Balanced AVL Tree:" << endl;
avl.show(r, 1);
cout<<endl;
break;
case 3:
cout << "Inorder Traversal:" << endl;
avl.inorder(r);
cout << endl;
break;
case 4:
cout << "Preorder Traversal:" << endl;
avl.preorder(r);
cout << endl;
break;
case 5:
cout << "Postorder Traversal:" << endl;
avl.postorder(r);
cout << endl;
break;
case 6:
exit(1);
break;
default:
cout << "Wrong Choice" << endl;
}
}
return 0;
} Đầu ra
1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 13 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 15 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 5 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 11 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 4 Left-Left Rotation1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 8 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 3 Inorder Traversal: 4 5 8 10 11 13 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 4 Preorder Traversal: 10 5 4 8 13 11 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 5 Postorder Traversal: 4 8 5 11 16 15 13 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 14 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 3 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 7 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 9 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 52 Right-Right Rotation 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 6
