BFS sử dụng STL để mã hóa cạnh tranh trong C ++?

Duyệt tìm kiếm đầu tiên theo chiều rộng (BFS) là một thuật toán, được sử dụng để truy cập tất cả các nút của một biểu đồ nhất định. Trong thuật toán duyệt này, một nút được chọn và sau đó lần lượt tất cả các nút lân cận được truy cập. Sau khi hoàn thành tất cả các đỉnh liền kề, nó di chuyển tiếp để kiểm tra các đỉnh khác và kiểm tra lại các đỉnh liền kề của nó.

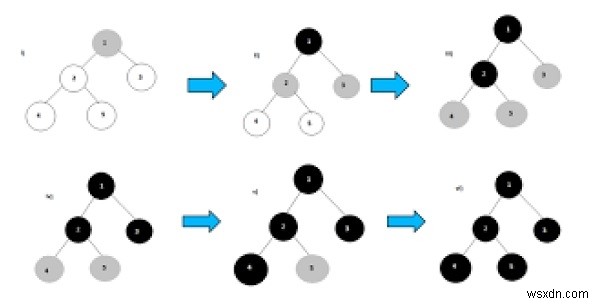
Trong Mã hóa cạnh tranh, chúng ta phải giải quyết các vấn đề rất nhanh. Chúng ta sẽ sử dụng STL (Standard Library of C ++) để thực hiện thuật toán này, chúng ta cần sử dụng cấu trúc dữ liệu Queue. Tất cả các đỉnh liền kề được thêm vào hàng đợi, khi tất cả các đỉnh liền kề được hoàn thành, một mục sẽ được xóa khỏi hàng đợi và bắt đầu đi ngang qua đỉnh đó một lần nữa.

Trong Đồ thị, đôi khi chúng ta có thể nhận được một số chu kỳ, vì vậy chúng ta sẽ sử dụng một mảng để đánh dấu thời điểm một nút đã được truy cập hay chưa.

Input : The Adjacency matrix of the graph.
A B C D E F
A 0 1 1 1 0 0
B 1 0 0 1 1 0
C 1 0 0 1 0 1
D 1 1 1 0 1 1
E 0 1 0 1 0 1
F 0 0 1 1 1 0
Output : BFS Traversal: B A D E C F

Thuật toán

bfs (đỉnh, bắt đầu)

Đầu vào - Danh sách các đỉnh và đỉnh bắt đầu.

Đầu ra - Đi qua tất cả các nút, nếu đồ thị được kết nối.

Begin
   define an empty queue que
   at first mark all nodes status as unvisited
   add the start vertex into the que
   while que is not empty, do
      delete item from que and set to u
      display the vertex u
      for all vertices 1 adjacent with u, do
         if vertices[i] is unvisited, then
            mark vertices[i] as temporarily visited
            add v into the queue
         mark
      done
      mark u as completely visited
   done
End

Ví dụ

#include<iostream>
#include<queue>
#define NODE 6
using namespace std;
class node {
   public:
      int val;
      int state; //status
};
int graph[NODE][NODE] = {
   {0, 1, 1, 1, 0, 0},
   {1, 0, 0, 1, 1, 0},
   {1, 0, 0, 1, 0, 1},
   {1, 1, 1, 0, 1, 1},
   {0, 1, 0, 1, 0, 1},
   {0, 0, 1, 1, 1, 0}
};
void bfs(node *vert, node s) {
   node u;
   int i, j;
   queue<node> que;
   for(i = 0; i<NODE; i++) {
      vert[i].state = 0; //not visited
   }
   vert[s.val].state = 1;//visited
   que.push(s); //insert starting node
   while(!que.empty()) {
      u = que.front(); //delete from queue and print
      que.pop();
      cout << char(u.val+'A') << " ";
      for(i = 0; i<NODE; i++) {
         if(graph[i][u.val]) {
            //when the node is non-visited
            if(vert[i].state == 0) {
               vert[i].state = 1;
               que.push(vert[i]);
            }
         }
      }
      u.state = 2;//completed for node u
   }
}
int main() {
   node vertices[NODE];
   node start;
   char s;
   for(int i = 0; i<NODE; i++) {
      vertices[i].val = i;
   }
   s = 'B';//starting vertex B
   start.val = s-'A';
   cout << "BFS Traversal: ";
   bfs(vertices, start);
   cout << endl;
}

Đầu ra

BFS Traversal: B A D E C F