Ở đây chúng ta sẽ thấy một vấn đề, trong bài toán này, một cạnh của cây và một tổng S được cho trước. Nhiệm vụ là gán trọng số cho tất cả các trọng số khác, sao cho đường đi dài nhất về trọng lượng được giảm thiểu. Tổng trọng số được gán cho nó giống như "S".
Cách tiếp cận rất đơn giản. Thuộc tính của cây mà một đường đi có thể có tối đa hai nút lá trong đó. Điều đó sẽ được sử dụng để có được giải pháp. Vì vậy, nếu chúng ta chỉ gán trọng số cho các cạnh nối các nút lá và gán các cạnh khác bằng 0. Khi đó mọi cạnh kết nối với các nút lá sẽ được gán là

Vì một đường dẫn có thể chứa tối đa hai nút lá, do đó đường dẫn dài nhất sẽ là
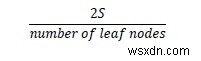
Ví dụ
#include<iostream>
#include<vector>
using namespace std;
void insertEdge(int u, int v, vector<int> adj[]) {
adj[u].push_back(v);
adj[v].push_back(u);
}
long double pathLength(vector<int> adj[], int sum, int n) {
int count = 0;
for (int i = 1; i <= n; i++) {
if (adj[i].size() == 1)
count++;
}
long double ans = 2.0 * (long double)(sum / (long double)(count));
return ans;
}
int main() {
int n = 6;
vector<int> adj[n + 1];
insertEdge(1, 2, adj);
insertEdge(2, 3, adj);
insertEdge(2, 4, adj);
insertEdge(4, 5, adj);
insertEdge(4, 6, adj);
int sum = 1;
cout << pathLength(adj, sum, n);
} Đầu ra
0.5
