Computer >> Máy Tính >  >> Lập trình >> C ++

Số lần lật tối thiểu để chuyển đổi ma trận nhị phân thành ma trận 0 trong C ++

Giả sử chúng ta có một ma trận nhị phân m x n. Trong một bước, chúng ta có thể chọn một ô và lật bit của nó và tất cả bốn ô lân cận của nó nếu chúng có mặt. Chúng ta phải tìm số bước tối thiểu cần thiết để chuyển đổi mat thành ma trận không. Nếu không có giải pháp nào, hãy trả về -1.

Vì vậy, nếu đầu vào đã cho giống như [[0,0], [0,1]], sự thay đổi sẽ giống như -

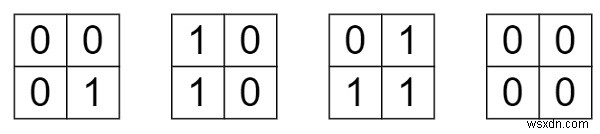
Số lần lật tối thiểu để chuyển đổi ma trận nhị phân thành ma trận 0 trong C ++

Vì vậy, chúng ta cần 3 bước, đầu ra sẽ là 3.

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • n:=số hàng, m:=số cột, x:=0
  • để khởi tạo i:=0, khi i
  • để khởi tạo j:=0, khi j
  • để khởi tạo j:=0, khi j
  • x:=x + mat shift trái [i] [j] value (i * m) + j) số lần
  • Xác định một mảng dp với 2 ^ (n * m) ô, điền vào ô này bằng -1
  • dp [x]:=0
  • Xác định một hàng đợi q
  • chèn x vào q
  • while (q không trống), do -
  • current:=phần tử đầu tiên của q, xóa phần tử khỏi q
  • nếu dòng điện bằng 0, thì -
    • trả về dp [hiện tại]
  • để khởi tạo i:=0, khi i
  • để khởi tạo j:=0, khi j
  • temp:=current
  • temp:=temp XOR 2 ^ (i * m) + j)
  • để khởi tạo k:=0, khi k <4, cập nhật (tăng k lên 1), thực hiện -
    • ni:=i + dir [k] [0]
    • nj:=j + dir [k] [1]
    • nếu ni <0 hoặc nj <0 hoặc ni> =n hoặc nj> =m, thì -
      • Bỏ qua phần sau, chuyển sang phần lặp tiếp theo
      • temp:=temp XOR 2 ^ (ni * m) + nj)
  • nếu dp [temp] giống -1, thì -
    • dp [temp]:=dp [current] + 1
    • chèn tạm thời vào q
  • trả về -1

    • Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

    Ví dụ 

    #include <bits/stdc++.h>
using namespace std;
int dir[4][2] = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
class Solution {
public:
   int minFlips(vector<vector<int>>& mat) {
      int n = mat.size();
      int m = mat[0].size();
      int x = 0;
      for(int i = 0; i < n; i++){
         for(int j = 0; j < m; j++){
            x += (mat[i][j] << ((i * m) + j));
         }
      }
      vector < int > dp(1 << (n*m), -1);
      dp[x] = 0;
      queue <int> q;
      q.push(x);
      while(!q.empty()){
         int current = q.front();
         q.pop();
         if(current == 0)return dp[current];
         for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
               int temp = current;
               temp ^= (1 << ((i *m) + j));
               for(int k = 0; k < 4; k++){
                  int ni = i + dir[k][0];
                  int nj = j + dir[k][1];
                  if(ni < 0 || nj < 0 || ni >= n || nj >= m)continue;
                  temp ^= (1 << ((ni *m) + nj));
               }
               if(dp[temp] == -1){
                  dp[temp] = dp[current] + 1;
                  q.push(temp);
               }
            }
         }
      }
      return -1;
   }
};
main(){
   Solution ob;
   vector<vector<int>> v = {{0,0},{0,1}};
   cout << (ob.minFlips(v));
}

    Đầu vào 

    {{0,0},{0,1}}

    Đầu ra 

    3