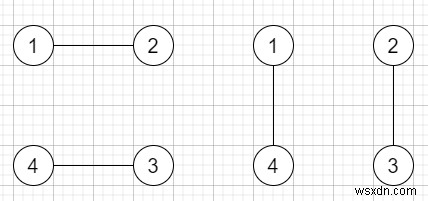
Bắt tay không vượt qua trong C ++

Giả sử chúng ta có một số chẵn n người đứng xung quanh một vòng tròn và mỗi người bắt tay với một người khác, do đó sẽ có tổng số n / 2 cái bắt tay. Chúng ta phải tìm ra số cách mà những cái bắt tay này có thể xảy ra sao cho không có cái bắt tay nào vượt qua. Các câu trả lời có thể rất lớn vì vậy hãy trả lại câu trả lời mod 10 ^ 9 + 7.

Vì vậy, nếu đầu vào là n =2, thì đầu ra sẽ là 1

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

m:=10 ^ 9 + 7
Xác định một mảng dp có kích thước (n + 1)
dp [0]:=1
để khởi tạo i:=0, khi i <=n, hãy cập nhật i:=i + 2, do -
- để khởi tạo j:=0, khi j <=i-2, cập nhật j:=j + 2, do -
  - dp [i]:=dp [i] + (dp [j] mod m * dp [i - 2 - j] mod m)
  - dp [i]:=dp [i] mod m
trả về dp [n] mod m

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ

#include <bits/stdc++.h>
using namespace std;
const int m = 1e9+7;
typedef long long int lli;
class Solution {
   public:
   int numberOfWays(int n) {
      vector <lli> dp(n+1);
      dp[0] = 1;
      for(int i = 0; i <= n; i+=2 ){
         for(int j =0 ; j <= i-2; j+=2){
            dp[i] += (dp[j]%m * dp[i-2-j]%m)%m;
            dp[i]%=m;
         }
      }
      return dp[n]%m;
   }
};
main(){
   Solution ob;
   cout << (ob.numberOfWays(2));
}

Bắt tay không vượt qua trong C ++

Ví dụ

Đầu vào

Đầu ra