Nhiệm vụ được giao là tìm số ô vuông tối đa có cạnh ‘a’ có thể nằm gọn trong một tam giác cân góc cho trước có đáy là ‘s’ (Một tam giác cân có ít nhất 2 cạnh bằng nhau).
Bây giờ chúng ta hãy hiểu những gì chúng ta phải làm bằng cách sử dụng một ví dụ:
Đầu vào
s=5, a=1
Đầu ra
10
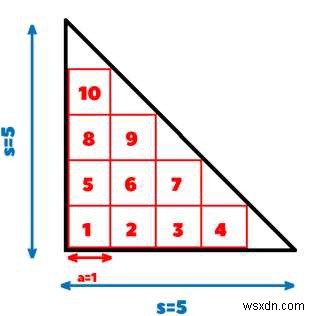
Giải thích - Số ô vuông trong cơ số có thể được tính bằng cách chia s cho a và trừ 1. Vậy số ô vuông trong cơ số =5/1 - 1 =4.
Tương tự khi 4 ô vuông dưới cùng được đặt thì chúng ta sẽ có được một tam giác cân mới với cơ sở là (s-a) và sau đó chúng ta lặp lại quy trình tương tự và lấy 3 hình vuông và cứ tiếp tục như vậy cho đến khi một hình vuông duy nhất được đặt ở trên cùng.
Đầu vào
s=7, a=2
Đầu ra
3
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau
-
Để tìm số ô vuông lớn nhất, chúng ta sẽ phải bắt đầu từ đáy của hình tam giác và tìm ra số ô vuông.
-
Để tìm số hình vuông, chúng ta sẽ chia cơ số s cho cạnh của hình vuônga và lấy nó trừ đi 1 =s / a - 1.
-
Sau đó, nó sẽ để lại cho chúng ta một tam giác cân khác với cơ sở (s - a) sẽ biến đổi một hình vuông nhỏ hơn hàng trước bên dưới nó mà chúng ta có thể tính toán theo cách sau -
Số bình phương ở hàng tiếp theo =(s - a) / a - 1 =(s / a - a / a) - 1 =s / a - 1 - 1 =s / a - 2 =số lượng ít hơn hàng trước.
-
Số ô vuông tiếp tục giảm cho đến khi bằng 1, do đó chúng ta chỉ phải tìm số ô vuông trong hàng cơ sở và sử dụng công thức cộng các số tự nhiên để tìm tổng cuối cùng là -
(n) * (n + 1) / 2
Trong trường hợp này, công thức trở thành - ((s / a) - 1) * (s / a) / 2
Ví dụ
#include<bits/stdc++.h>
using namespace std;
int Max(int s, int a){
//formula for calculating maximum squares
return ((s / a) - 1) * (s / a) / 2;
}
//Main function
int main(){
int s = 5, a = 1;
cout <<"Maximum squares possible are: "<<Max(s,a);
return 0;
} Đầu ra
10
