Computer >> Máy Tính >  >> Lập trình >> C ++

Chương trình tìm số bước tối thiểu cần thiết để bắt đối thủ trong C ++

Giả sử chúng ta có một danh sách các cạnh cây có dạng [u, v], điều này chỉ ra rằng có một cạnh vô hướng giữa u và v. Và chúng ta cũng có hai giá trị x và y. Nếu chúng ta đang ở nút x và đối thủ của chúng ta ở nút y. Trong vòng đầu tiên, chúng tôi di chuyển, sau đó trong vòng tiếp theo đối thủ di chuyển và như vậy. Đối phương có thể chọn không di chuyển trong một hiệp đấu. Chúng ta phải tìm ra số hiệp tối thiểu mà chúng ta cần để bắt được đối thủ.

Vì vậy, nếu đầu vào giống như các cạnh =[[0, 1], [0, 2], [1, 3], [1, 4]], x =0, y =3, thì đầu ra sẽ là 3, như lúc đầu, chúng tôi di chuyển từ nút 0 sang 1. Sau đó, đối thủ ở lại nút hiện tại 3. Sau đó, chúng tôi chuyển sang nút 3.

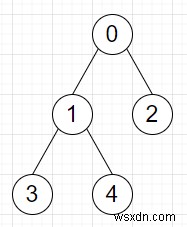
Chương trình tìm số bước tối thiểu cần thiết để bắt đối thủ trong C ++

Để giải quyết vấn đề này, chúng tôi sẽ làm theo các bước sau -

  • N:=1 ^ 5 + 5

  • Xác định một mảng được truy cập có kích thước:N và một mảng khác được truy cập2 có kích thước:N điền chúng bằng −1

  • tạo biểu đồ danh sách kề cho N nút

  • đối với mỗi cạnh của nó trong danh sách cạnh, hãy thực hiện

    • chèn nó [v] vào cuối biểu đồ [it [u]]

    • chèn nó [u] vào cuối biểu đồ [it [v]]

  • Xác định một hàng đợi w

  • chèn u vào q

  • đã ghé thăm [u]:=0

  • trong khi q không trống, thực hiện -

    • node:=phần tử đầu tiên của q

    • xóa phần tử khỏi q

    • cho mỗi nút, nó trong biểu đồ [node]

      • nếu được truy cập [nó] giống với −1, thì -

        • đã ghé thăm [nó]:=đã ghé thăm [node] + 1

        • chèn nó vào q

  • chèn v vào q

  • ret:=0

  • đã thăm 2 [v]:=0

  • trong khi q không trống), do -

    • node:=phần tử đầu tiên của q

    • xóa phần tử khỏi q

    • ret:=tối đa ret và 2 * (đã truy cập [nút])

    • cho mỗi nút, nó trong biểu đồ [node]

      • nếu đã thăm 2 [nó] giống -1 và đã thăm2 [nút] + 2 <đã thăm [nó] thì -

        • đã thăm 2 [nó]:=đã thăm2 [nút] + 1

        • chèn nó vào q

  • trả lại ret

Hãy cùng chúng tôi xem cách triển khai sau để hiểu rõ hơn -

Ví dụ 

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int visited[N];
int visited2[N];
vector<int> graph[N];
class Solution {
   public:
   int solve(vector<vector<int>>& edges, int u, int v) {
      memset(visited, −1, sizeof visited);
      memset(visited2, −1, sizeof visited2);
      for (int i = 0; i < N; i++)
      graph[i].clear();
      for (auto& it : edges) {
         graph[it[0]].push_back(it[1]);
         graph[it[1]].push_back(it[0]);
      }
      queue<int> q;
      q.push(u);
      visited[u] = 0;
      while (!q.empty()) {
         int node = q.front();
         q.pop();
         for (auto& it : graph[node]) {
            if (visited[it] == −1) {
               visited[it] = visited[node] + 1;
               q.push(it);
            }
         }
      }
      q.push(v);
      int ret = 0;
      visited2[v] = 0;
      while (!q.empty()) {
         int node = q.front();
         q.pop();
         ret = max(ret, 2 * (visited[node]) − 1);
         for (auto& it : graph[node]) {
            if (visited2[it] == −1 && visited2[node] + 2 <
            visited[it]) {
               visited2[it] = visited2[node] + 1;
               q.push(it);
            }
         }
      }
      return ret;
   }
};
int solve(vector<vector<int>>& edges, int u, int v) {
   return (new Solution())−>solve(edges, u, v);
}
int main(){
   vector<vector<int>> edge = {{0, 1},{0, 2},{1, 3},{1, 4}};
   int x = 0, y = 3;
   cout << solve(edge, x, y);
}

Đầu vào 

[
   [0, 1],
   [0, 2],
   [1, 3],
   [1, 4]
], 0, 3

Đầu ra 

3