Cho một cây nhị phân với trọng số của các nút là số. Mục đích là tìm số nút có trọng số sao cho số đó là số Fibonacci. Các số trong chuỗi Fibonacci là:0, 1, 1, 2, 3, 5, 8, 13…. Số thứ n là tổng của (n − 1) th và (n − 2) th. Nếu trọng lượng là 13 thì đó là số Fibonacci nên nút sẽ được tính.
Ví dụ
Đầu vào
nhiệt độ =1. Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -
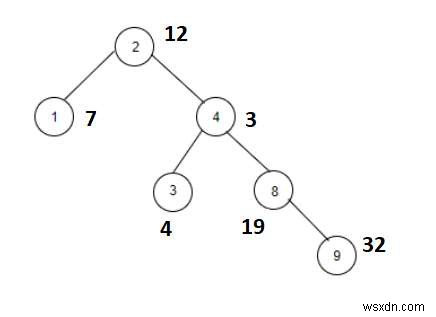
Đầu ra
Count the nodes whose sum with X is a Fibonacci number are: 3
Giải thích
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| Trọng lượng | Trọng lượng + temp =fibonacci | Có / Không | |
|---|---|---|---|
| 2 | 12 | 12 + 1 =13 | vâng |
| 1 | 7 | 7 + 1 =8 | vâng |
| 4 | 3 | 3 + 1 =4 | không |
| 3 | 4 | 4 + 1 =5 | vâng |
| 8 | 19 | 19 + 1 =20 | không |
| 9 | 32 | 32 + 1 =33 | không |
Đầu vào
temp =3. Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -
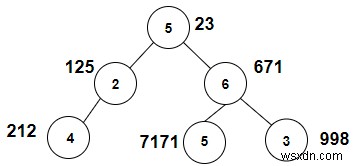
Đầu ra
Count the nodes whose sum with X is a Fibonacci number are: 3
Giải thích
we are given with the tree nodes and the weights associated with each node. Now we check whether the temp+weight is a Fibonacci number or not.
| Trọng lượng | Trọng lượng + temp =fibonacci | Có / Không | |
|---|---|---|---|
| 5 | 23 | 23 + 3 =26 | không |
| 2 | 125 | 125 + 3 =128 | không |
| 6 | 671 | 671 + 3 =674 | không |
| 4 | 212 | 212 + 3 =215 | không |
| 5 | 7171 | 7171 + 3 =7174 | không |
| 3 | 998 | 998 + 3 =1001 | không |
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau -
Trong cách tiếp cận này, chúng tôi sẽ áp dụng DFS trên biểu đồ của cây để duyệt qua nó và kiểm tra xem trọng số của nút và tạm thời có cộng tối đa một số fibonacci hay không. Lấy hai vectorsNode_Weight (100) và edge_graph [100] cho mục đích này.
-
Khởi tạo Node_Weight [] với trọng số của các nút.
-
Tạo cây bằng cách sử dụng vector edge_graph.
-
Lấy Fibonacci biến toàn cục và khởi tạo nó bằng 0. Lấy nhiệt độ biến toàn cục khác.
-
Hàm check_square (val kép dài) nhận một số nguyên và trả về true nếu val là một hình vuông hoàn hảo.
-
Lấy val_1 =sqrt (val)
-
Bây giờ nếu (val_1 - floor (val_1) ==0) trả về true thì tổng là một hình vuông hoàn hảo, trả về true.
-
Nếu không thì trả về false.
-
Hàm check_Fibonacci (int num) nhận một số và trả về true nếu đó là số afibonacci.
-
Khởi tạo fib với 5 * num * num.
-
Nếu check_square ((fib + 4)) || check_square ((fib - 4)) cho kết quả true sau đó trả về true.
-
Nếu không thì trả về false.
-
Hàm Fibonacci_number (int node, int root) trả về số lượng các nút với X là số Fibonacci.
-
Nếu if (check_Fibonacci (Node_Weight [node] + temp)) trả về true thì incrementFibonacci.
-
Cây ngang trong vector edge_graph [node] sử dụng vòng lặp for.
-
Gọi Fibonacci_number (nó, nút) cho nút tiếp theo trong vectơ.
-
Ở cuối tất cả các hàm, chúng ta sẽ có Fibonacci là số nút có trọng số có tổng với tạm thời là số fibonacci.
Ví dụ
#include <bits/stdc++.h>
using namespace std;
vector<int> Node_Weight(100);
vector<int> edge_graph[100];
int Fibonacci = 0, temp;
bool check_square(long double val){
long double val_1 = sqrt(val);
if(val_1 − floor(val_1) == 0){
return true;
}
return false;
}
bool check_Fibonacci(int num){
int fib = 5 * num * num;
if(check_square((fib + 4)) || check_square((fib − 4))){
return true;
}
return false;
}
void Fibonacci_number(int node, int root){
if(check_Fibonacci(Node_Weight[node] + temp)){
Fibonacci++;
}
for (int it : edge_graph[node]){
if(it == root){
continue;
}
Fibonacci_number(it, node);
}
}
int main(){
//weight of the nodes
Node_Weight[2] = 6;
Node_Weight[1] = 4;
Node_Weight[4] = 23;
Node_Weight[3] = 5;
Node_Weight[8] = 161;
Node_Weight[9] = 434;
//create graph edge
edge_graph[2].push_back(1);
edge_graph[2].push_back(4);
edge_graph[4].push_back(3);
edge_graph[4].push_back(8);
edge_graph[8].push_back(9);
temp = 3;
Fibonacci_number(2, 2);
cout<<"Count the nodes whose sum with X is a Fibonacci number are: "<<Fibonacci;
return 0;
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -
Count the nodes whose sum with X is a Fibonacci number are: 1
