Chúng ta được cung cấp một giá trị nguyên và một biến x và nhiệm vụ là xây dựng cây nhị phân và tìm các cặp có tổng bằng giá trị x đã cho.
Ví dụ
Đầu vào
int x =5, Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -

Đầu ra
Count of pairs in a binary tree whose sum is equal to a given value x are: 2
Giải thích
we are given with an array of integer values that is used to form a binary tree and we will check whether there is a pair present in a binary tree whose sum equals to the given value x which is 5. So, the pairs formed are (2, 3) and (1, 4).
Đầu vào
int x =8, Cây sẽ được tạo sau khi nhập các giá trị được đưa ra bên dưới -
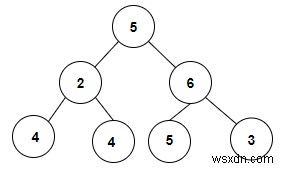
Đầu ra
Count of pairs in a binary tree whose sum is equal to a given value x are: 3
Giải thích
we are given with an array of integer values that is used to form a binary tree and we will check whether there is a pair present in a binary tree whose sum equals to the given value x which is 8. So, the pairs formed are (2, 6), (4, 4) and (5, 3).
Phương pháp tiếp cận được sử dụng trong chương trình dưới đây như sau -
-
Tạo cấu trúc của một nút có chứa phần dữ liệu và các con trỏ trái và phải sẽ trỏ đến cây con bên trái và bên phải.
-
Nhập một giá trị số nguyên và sử dụng chúng để tạo cây nhị phân bằng cách nhập dữ liệu vào nút thông qua con trỏ trái và phải.
-
Nhập giá trị x sẽ được sử dụng để tính các cặp có tổng giá trị là x.
-
Tạo một hàm boolean để kiểm tra xem tổng các cặp có phải là x hay không.
-
Bên trong hàm, hãy kiểm tra xem root có phải là NULL hay không rồi trả về False
-
Kiểm tra IF root không bằng ptr và dữ liệu của root + data của ptr bằng x thì trả về True.
-
Gọi hàm kiểm tra đệ quy bằng cách chuyển con trỏ bên trái của gốc, ptr và giá trị x và cả con trỏ bên phải của x, ptr và x. Bây giờ, hãy kiểm tra xem có điều kiện nào trả về true hay không, sau đó trả về true.
-
Khác, trả về false.
-
Tạo một hàm total_pairs để tính toán số lượng các cặp có tổng là x
-
Bên trong hàm, kiểm tra xem ptr có phải là NULL không rồi trả về 0.
-
Gọi hàm kiểm tra bằng cách chuyển root, ptr và x làm đối số. NẾU hàm trả về true thì tăng giá trị của tổng các cặp lên 1
-
Gọi hàm total_pairs một cách đệ quy bằng cách truyền con trỏ gốc, con trỏ bên trái của ptr, x và tổng và cũng truyền con trỏ gốc, con trỏ bên phải của ptr, x và tổng.
-
In kết quả dưới dạng giá trị số nguyên được lưu trữ trong một tổng biến.
Ví dụ
#include <bits/stdc++.h>
using namespace std;
struct tree_node {
int data;
tree_node *left, *right;
};
tree_node* create_node(int data){
tree_node* newNode = (tree_node*)malloc(sizeof(tree_node));
newNode−>data = data;
newNode−>left = newNode−>right = NULL;
}
bool check(tree_node* root, tree_node* ptr, int x){
if(root==NULL){
return false;
}
if (root != ptr && ((root−>data + ptr−>data) == x)){
return true;
}
if (check(root−>left, ptr, x) || check(root−>right, ptr, x)){
return true;
}
return false;
}
void total_pairs(tree_node* root, tree_node* ptr, int x, int& total){
if(ptr == NULL){
return;
}
if(check(root, ptr, x) == true){
total++;
}
total_pairs(root, ptr−>left, x, total);
total_pairs(root, ptr−>right, x, total);
}
int main(){
int x = 5;
int total = 0;
tree_node* root = create_node(5);
root−>left = create_node(2);
root−>right = create_node(3);
root−>left−>left = create_node(1);
root−>left−>right = create_node(4);
root−>right−>left = create_node(6);
total_pairs(root, root, x, total);
total = total / 2;
cout<<"Count of pairs in a binary tree whose sum is equal to a given value x are: "<< total;
return 0;
} Đầu ra
Nếu chúng ta chạy đoạn mã trên, nó sẽ tạo ra kết quả sau -
Count of pairs in a binary tree whose sum is equal to a given value x are: 2
