Dudeney Numbers trong C ++

Một số toán học được định nghĩa trong lý thuyết số trong một cơ số đã cho là một số tự nhiên bằng lập phương hoàn hảo của một số tự nhiên khác sao cho tổng các chữ số của số tự nhiên thứ nhất bằng tổng các chữ số của số thứ hai (wikipedia).

Số được tìm thấy bởi Henry Dudeney . Công thức toán học của nó là -

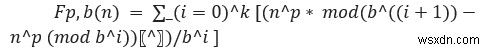
Ở đây, chúng ta được cung cấp một số nguyên n. Nhiệm vụ của chúng ta là kiểm tra xem số n đã cho có phải là số dudeney hay không.

Hãy lấy một ví dụ để hiểu vấn đề,

Đầu vào: N =17592

Đầu ra: Không

Giải thích:

Số đã cho không phải là số dudney.

Phương pháp tiếp cận Giải pháp -

Giải pháp nằm trong định nghĩa cơ bản của số dudeney. Một số là một số dudeney dựa trên thực tế là căn bậc hai của một số bằng tổng các chữ số của nó .

Thuật toán -

Bước 1: Kiểm tra xem n có phải là một khối hoàn hảo không.

Bước 2.1: Nếu CÓ, hãy kiểm tra xem căn bậc hai của n =tổng các chữ số của n.

Bước 2.2.1: Nếu CÓ, thì số là số Dudeney.

Bước 2.2.2: Nếu KHÔNG, thì số đó không phải là số Dudeney.

Bước 2.2: Nếu KHÔNG, thì số đó không phải là số Dudeney.

Chương trình C ++ để minh họa hoạt động của thuật toán của chúng tôi -

Ví dụ

#include <bits/stdc++.h>
using namespace std;

int calcDigitSum(int n){

   int digitSum = 0;
   int digitVal;
   while (n > 0) {
      digitVal = n % 10;
      digitSum += digitVal;
      n /= 10;
   }
   return digitSum;
   
}
int checkDudeney(int N) {
   
   int cubeRoot = int( round( cbrt(N) ) );
   
   if(pow(cubeRoot, 3.0) != N){
      return 0;
   }

   int sumOfDigit = calcDigitSum(N);
   
   if (cubeRoot != sumOfDigit)
      return 0;

   return 1;
}

int main() {
   int N = 104323;
   cout<<"The number "<<N;
   if (checkDudeney(N))
      cout<<" is a dudeney number.";
   else
      cout<<" is not a dudeney number.";
   return 0;
}

Đầu ra -

The number 104323 is not a dudeney number.