Để giải quyết một vấn đề trong đó chúng ta được đưa ra một cây nhị phân. Bây giờ chúng ta cần tìm con đường có số khúc cua lớn nhất. tức là, một khúc cua được coi là khi hướng của con đường thay đổi từ trái sang phải hoặc ngược lại, chẳng hạn
Đầu vào -
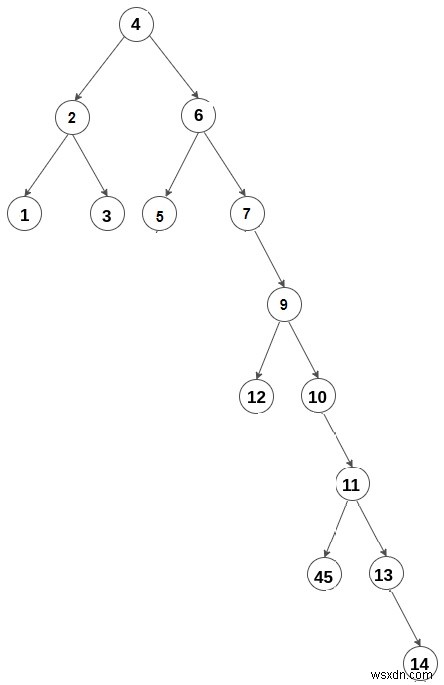
Đầu ra -
6
Bây giờ trong cách tiếp cận này, chúng ta sẽ đi ngang qua cây và theo dõi các chuyển động trước đó. Nếu hướng thay đổi, chúng tôi chỉ cần cập nhật số lượng khúc cua và sau đó chúng tôi tìm ra giá trị lớn nhất.
Phương pháp tiếp cận để tìm giải pháp
Trong cách tiếp cận này, chúng tôi sẽ đi qua tất cả các con đường và chúng tôi tìm thấy số khúc cua tối đa mà chúng tôi cập nhật câu trả lời của mình.
Ví dụ
#include <bits/stdc++.h>
using namespace std;
struct Node { // structure of our node
int key;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int key){ // initializing our node
struct Node* node = new Node();
node->left = NULL;
node->right = NULL;
node->key = key;
return node;
}
void maximumBends(struct Node* node,char direction, int bends,
int* maxBends, int soFar,int* len){
if (node == NULL) // if null is reached
return;
if (node->left == NULL && node->right == NULL) { // if we reach the leaf node then
//we check if we have to update our answer or not
if (bends > *maxBends) {
*maxBends = bends;
*len = soFar;
}
}
else {
if (direction == 'l') { // current direction is left
maximumBends(node->left, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->right, 'r',bends + 1, maxBends,soFar + 1, len); // if we change direction so bend also increases
}
else {
maximumBends(node->right, direction,bends, maxBends,soFar + 1, len);
maximumBends(node->left, 'l',bends + 1, maxBends,soFar + 1, len); // same as when direction was left
}
}
}
int main(){
struct Node* root = newNode(10);
root->left = newNode(8);
root->right = newNode(2);
root->left->left = newNode(3);
root->left->right = newNode(5);
root->right->left = newNode(2);
root->right->left->right = newNode(1);
root->right->left->right->left = newNode(9);
int len = 0, bends = 0, maxBends = -1;
if(!root) // if tree is empty
cout << "0\n";
else{
if (root->left) // if left subtree exists
maximumBends(root->left, 'l',bends, &maxBends, 1, &len);
if (root->right) // if right subtree exists
maximumBends(root->right, 'r', bends,&maxBends, 1, &len);
cout << len << "\n";
}
return 0;
} Đầu ra
4
Giải thích về Quy tắc trên
Trong cách tiếp cận ở trên, chúng tôi chỉ đơn giản là đi qua tất cả các con đường và đếm khúc cua được tìm thấy cho đến nay khi chúng tôi đến cuối con đường. I.e nút lá, chúng tôi kiểm tra xem các khúc cua ở đây có lớn hơn mức tối đa trước đó bây giờ không nếu điều kiện là đúng, vì vậy chúng tôi cập nhật các khúc cua tối đa cũng như độ dài của đường dẫn đến độ dài mới này và đó là cách chương trình của chúng tôi tiến hành.
Kết luận
Trong hướng dẫn này, chúng tôi giải quyết một vấn đề để tìm độ dài Đường dẫn có số khúc cua tối đa. Chúng tôi cũng đã học chương trình C ++ cho vấn đề này và cách tiếp cận hoàn chỉnh (Bình thường) mà chúng tôi đã giải quyết vấn đề này. Chúng ta có thể viết cùng một chương trình bằng các ngôn ngữ khác như C, java, python và các ngôn ngữ khác. Chúng tôi hy vọng bạn thấy hướng dẫn này hữu ích.
